√ 円周角の定理 191140-円周角の定理 指導案
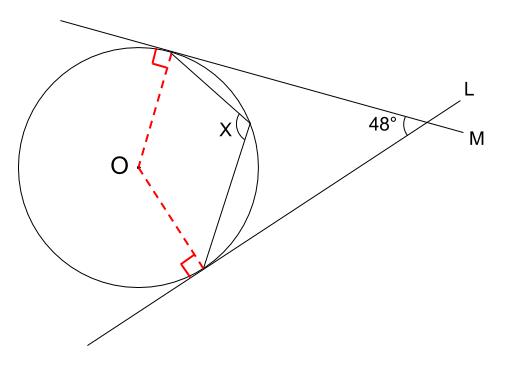
中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su
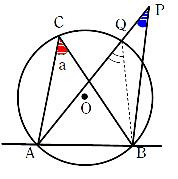
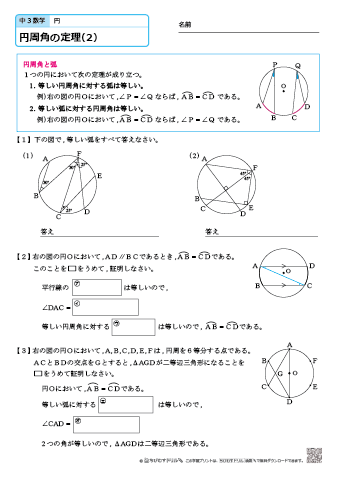
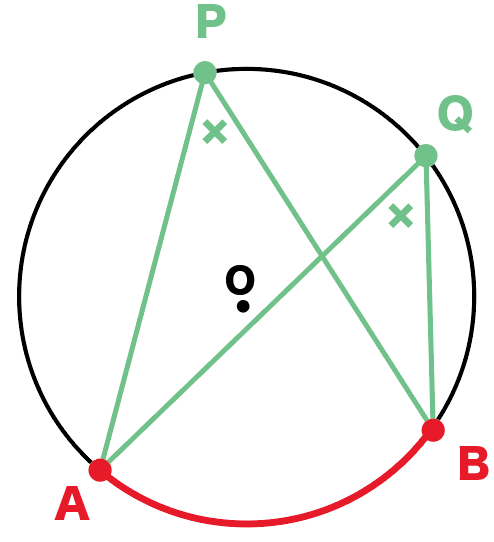
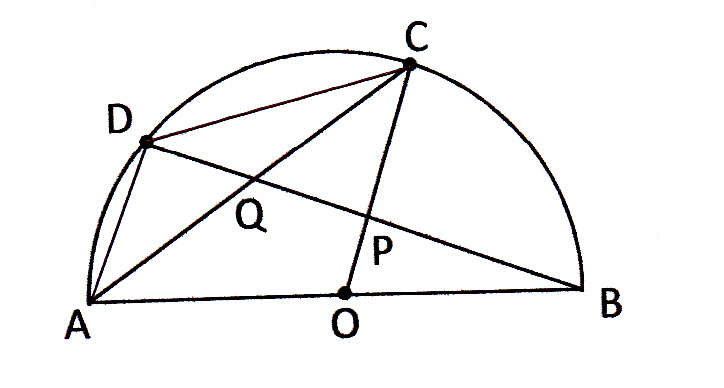
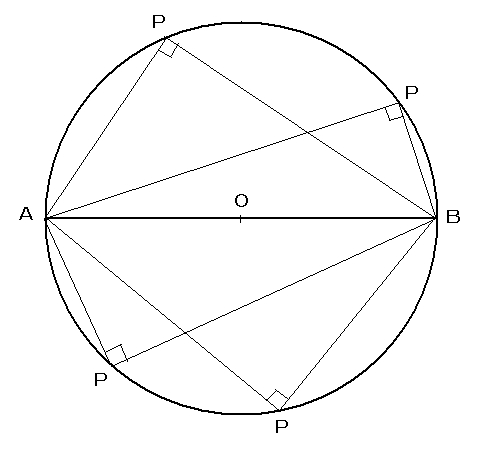
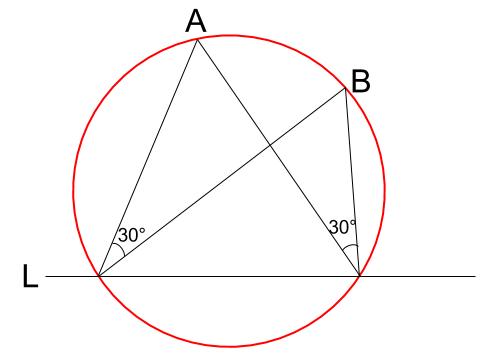
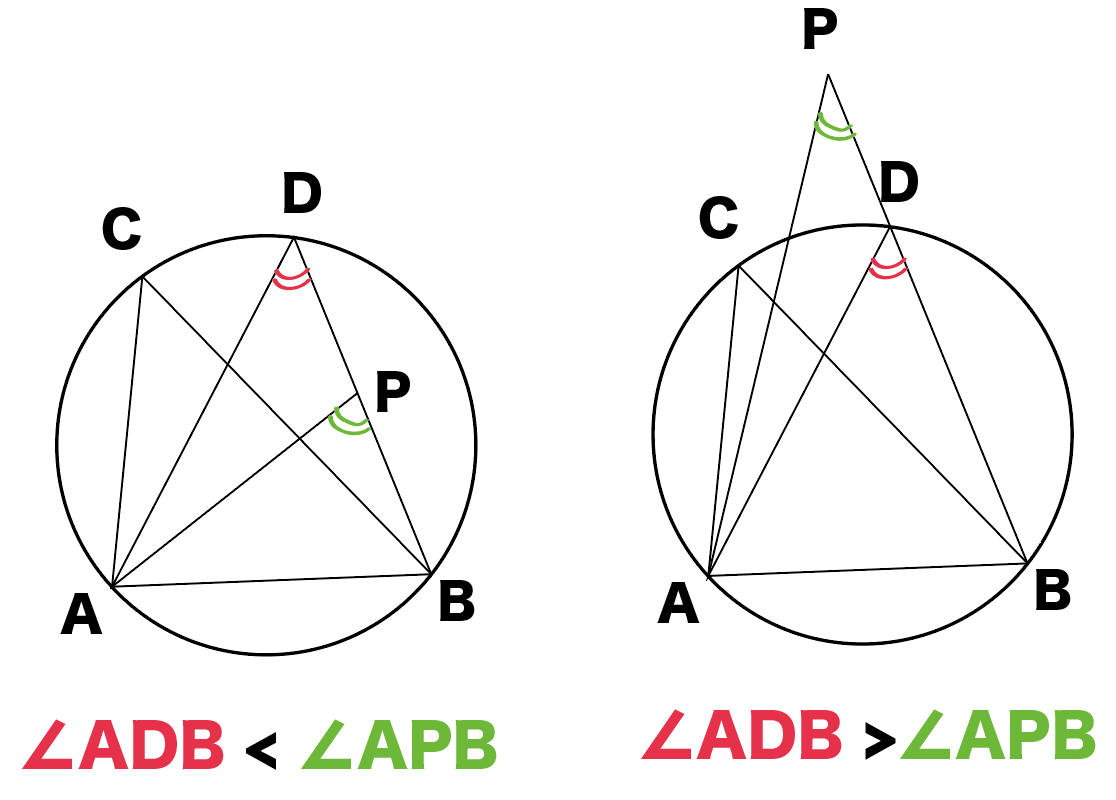
円周角の定理は,その逆の主張も成立します.これは,平面上の 4 4 点が同一周上にあるための判定法のひとつになっています. 証明は次の事実により従います. 一つの円周上に 3 3 点 A,B,C A, B, C があるとき,直線 AB A B について,点 C C と同じ側に点 P P 円周角の定理を応用したさまざまな定理 円周角の定理は,より難しいいろいろな定理の証明に使われます。例えば, タレスの定理 :円に内接する三角形のうち,斜辺の長さが円の直径と等しい三角形は直角三角形となります。これはタレスの定理と呼ばれ
円周角の定理 指導案
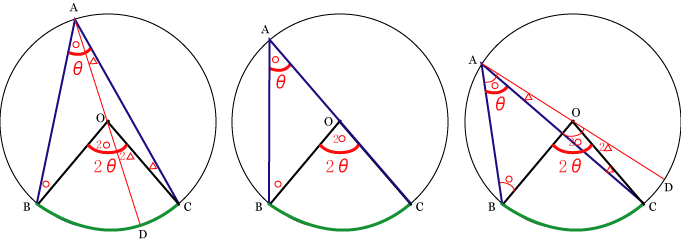
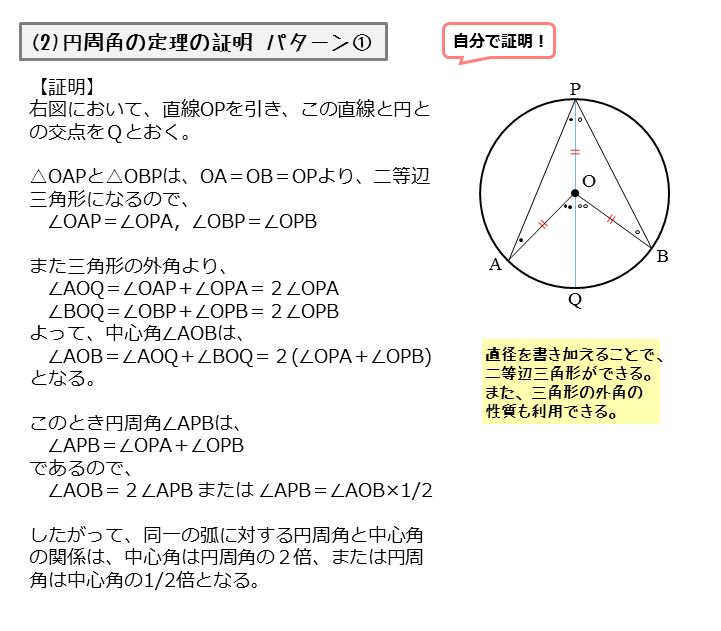
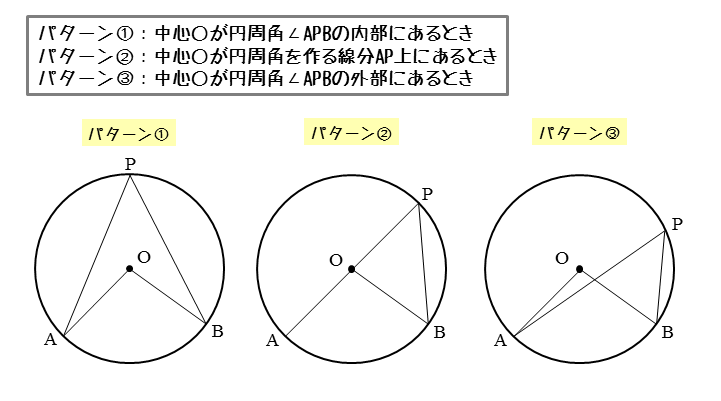
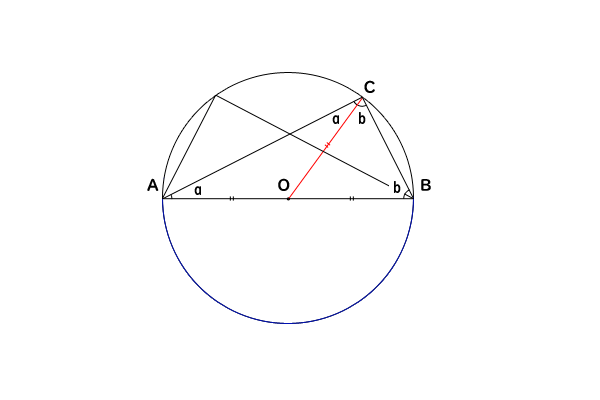
円周角の定理 指導案- 円周角の定理の証明② 中心を含むとき 次は以下のように、「ある1点から円周上の2点に伸ばした2直線の間に、中心が位置するとき」です。 三角形abc中に中心oが来るイメージです。 このとき、円周角の定理を証明するには、 ∠bac=½ ∠boc を証明すればいいわけです。 bcを結ぶ直線と「円周角の定理の証明」同様、『場合分け証明』になります 〔 ∠ABCが90°の場合 〕 ∠ABCが90°のとき、ACは直径 (円周角が90° ⇔ 直径より) ∴ OCは半径 OC ⊥ l (半径と接線は垂直に交わる より) ∠ACl = 90° ∠ABC = 90°(仮定より) ∴ ∠ACl = ∠ABC 外角の定理 ここで次に備えて、「外角の定理(スリッパ
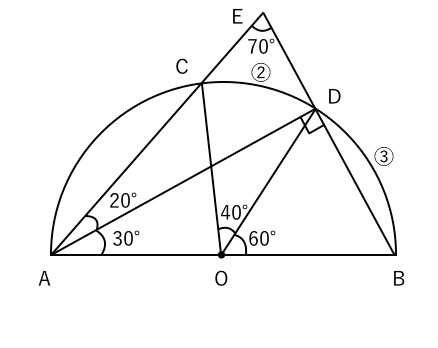
円周角と比の問題 苦手な数学を簡単に
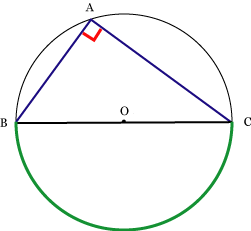
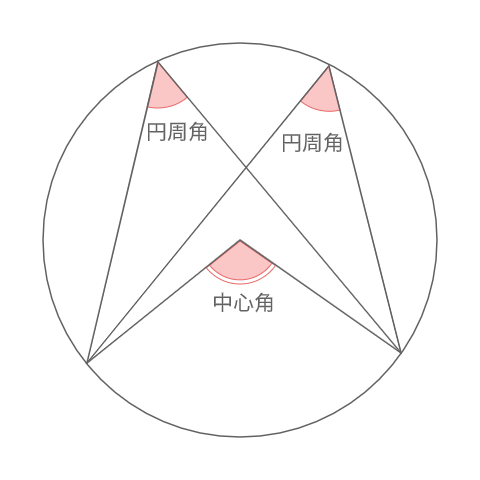
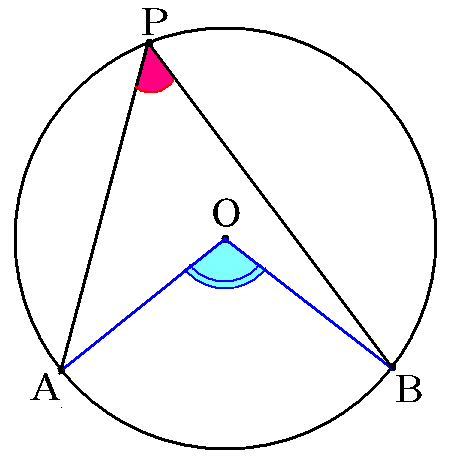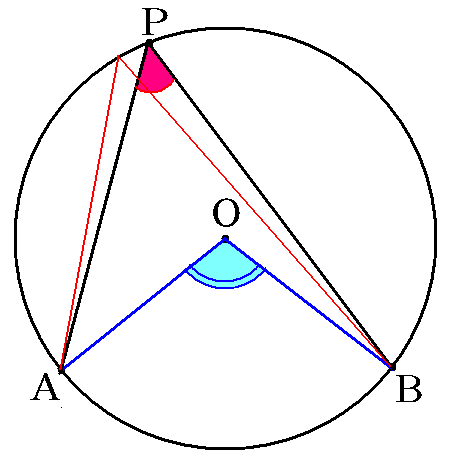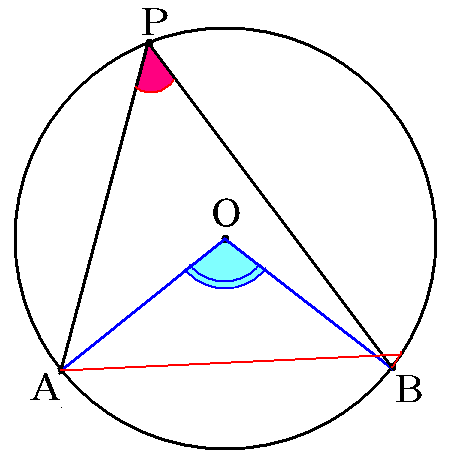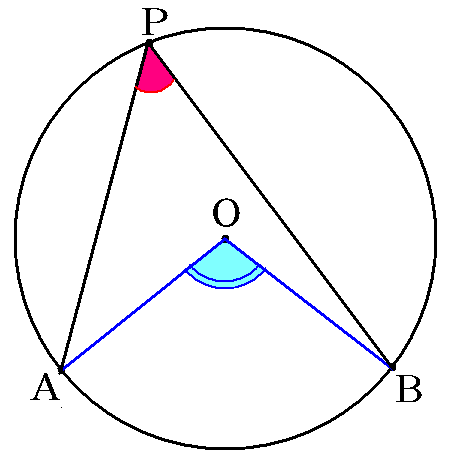
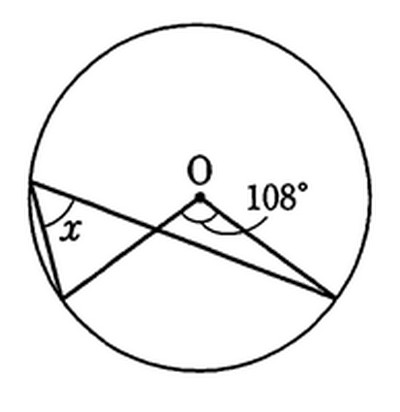
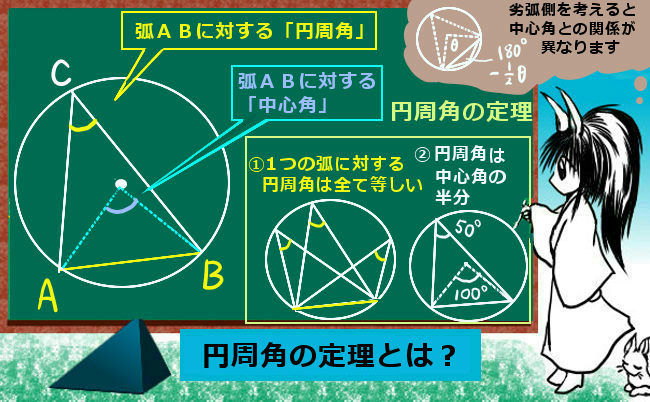
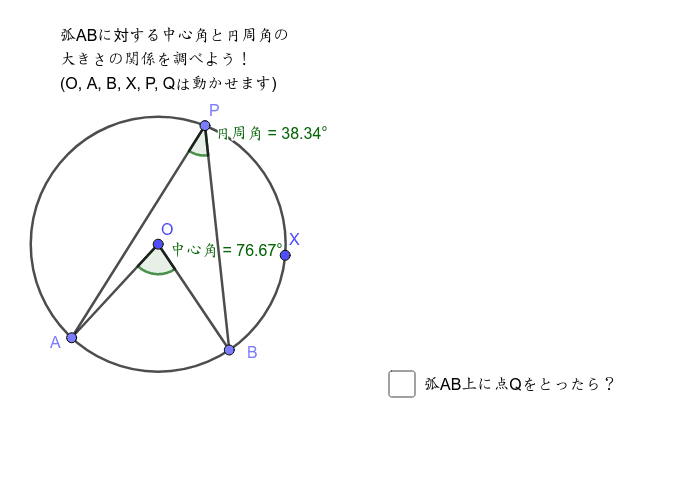
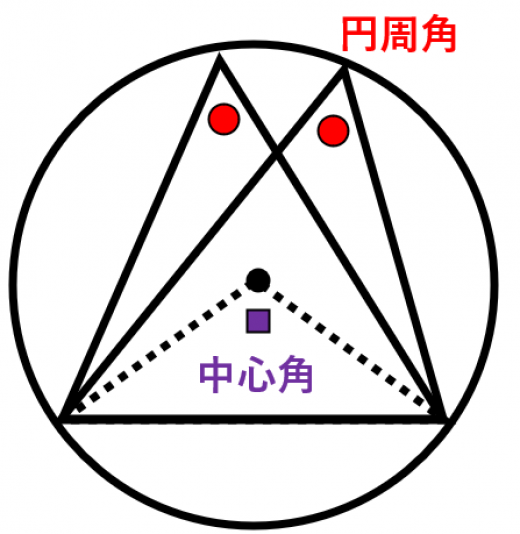
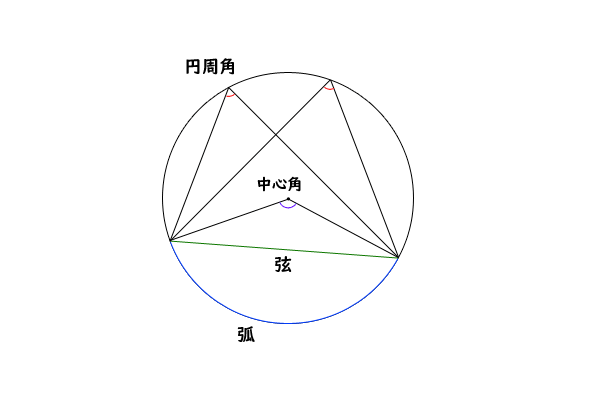
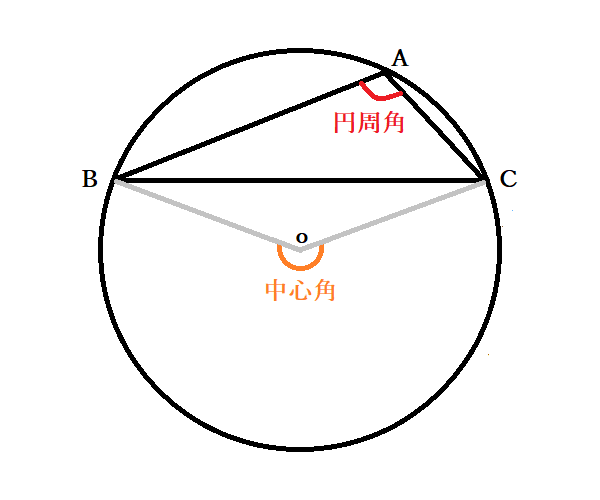
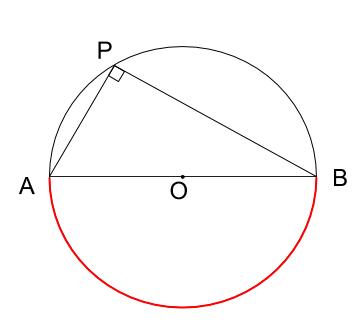
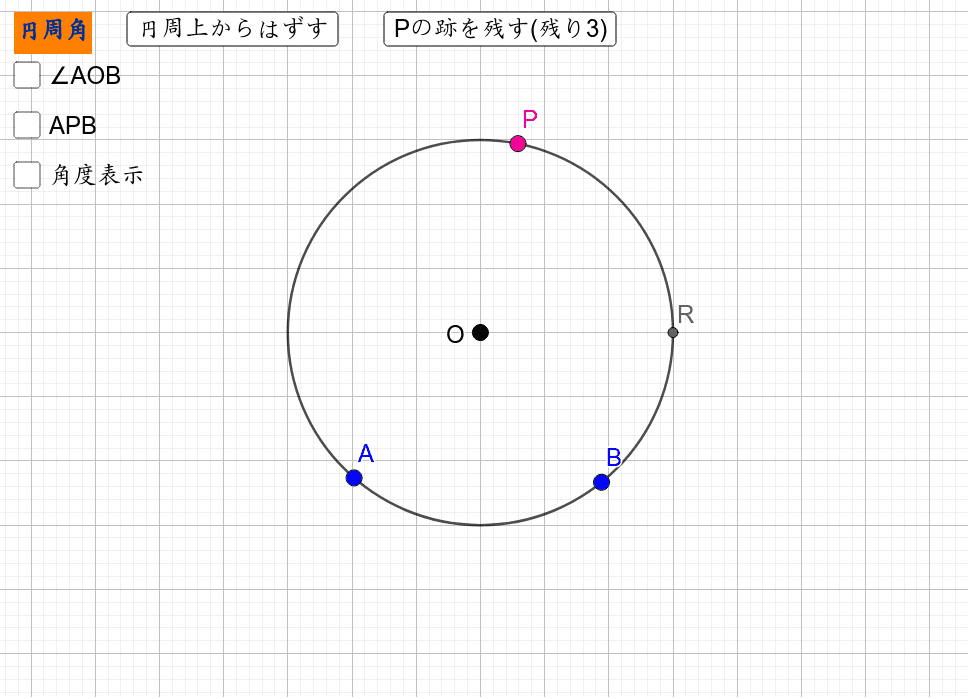
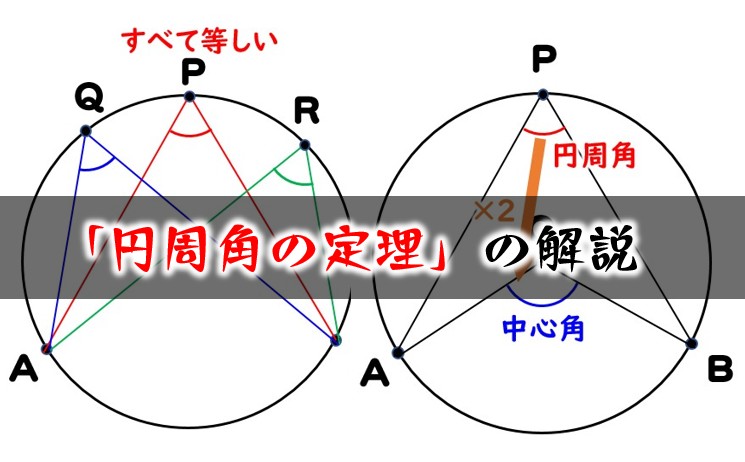
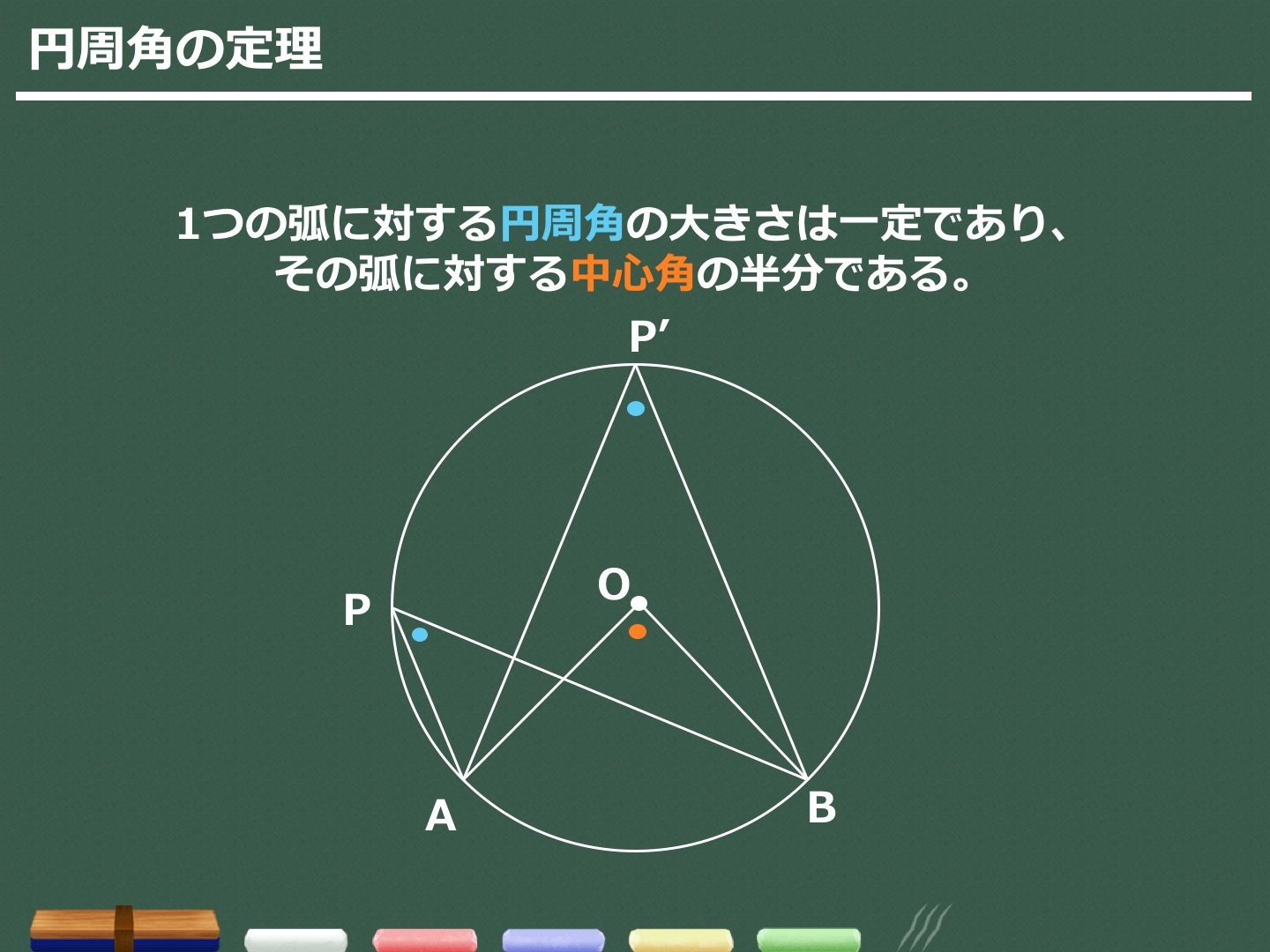
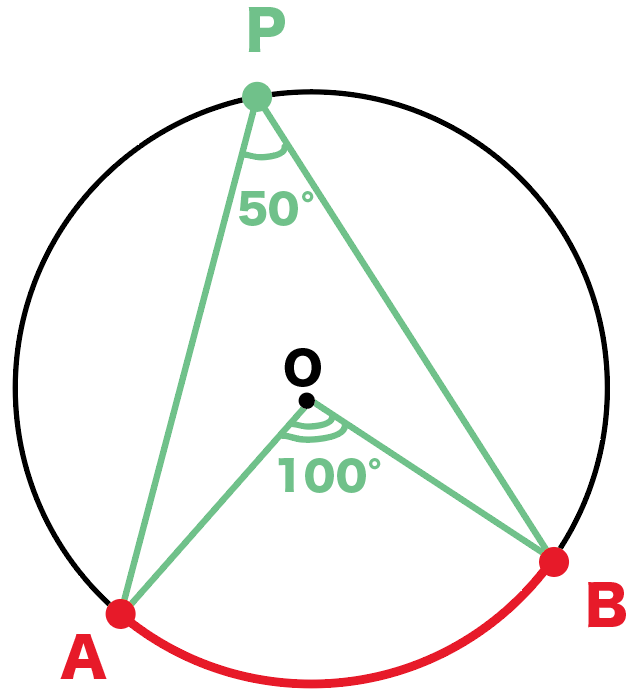
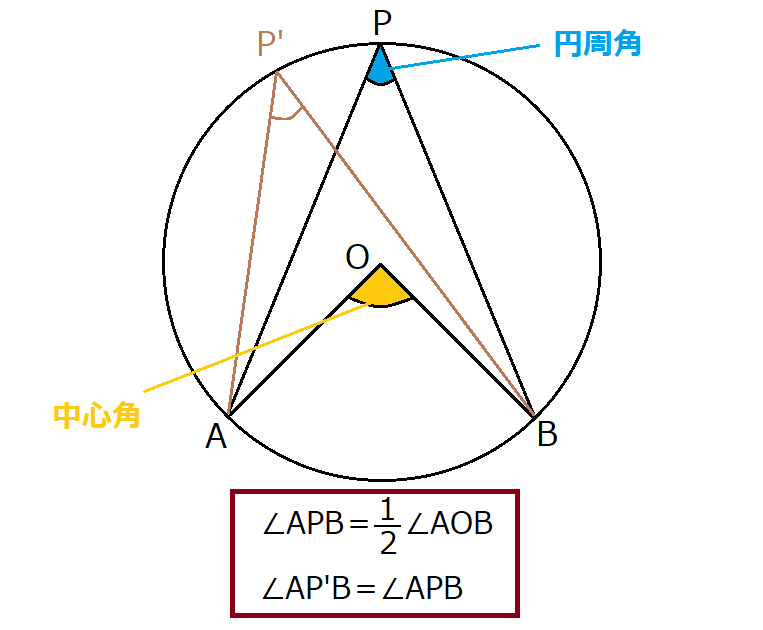
円周角の定理をあらわす以下の複素数平面の図を考えて、以下の式の形で円周角の定理があらわされることを計算して試してみましょう。 (注意) オイラーの定理「exp(iβ)=(cosβ+isinβ)」は、前提条件として使ってください。 この問題の目的はオイラーの定理を証明することでは無く一般に,高校入試問題では「円周角の定理」を覚えているだけでは,問題は解けません.この問題では,次の2つの定理を組み合わせて解いています. (1) 一つの弧に対する円周角は等しい. (2) 三角形の内角の和は180°になる. 問題2 (1) 右の図のよう円周角の定理 1つの弧に対する円周角の大きさは一定であり、その弧に対する中心角の半分である。 弧が直径の場合 今度は、上で説明した図形のうち、点a,点o,点cが一直線になる場合を考えてみます。 円周角の定理から明らかなことですが、中心角∠aocは180°となるので、円周角∠abcはその
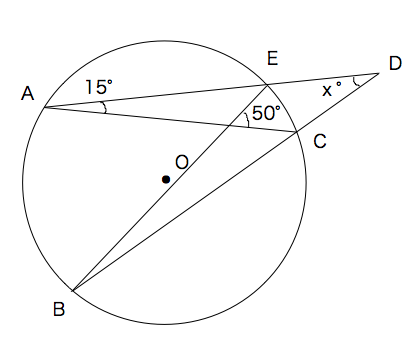
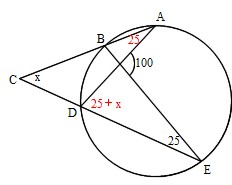
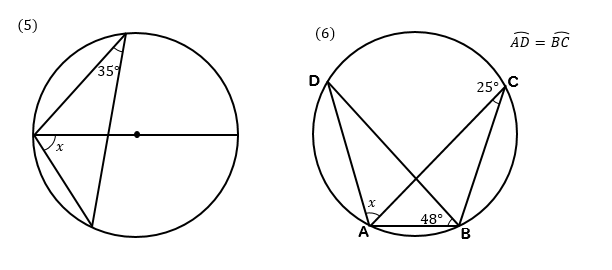
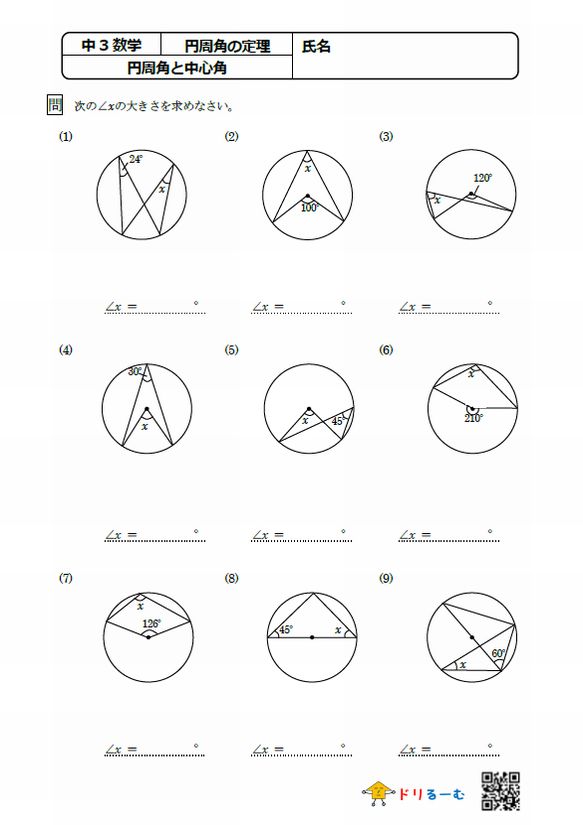
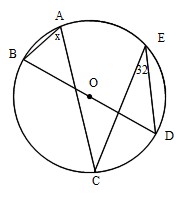
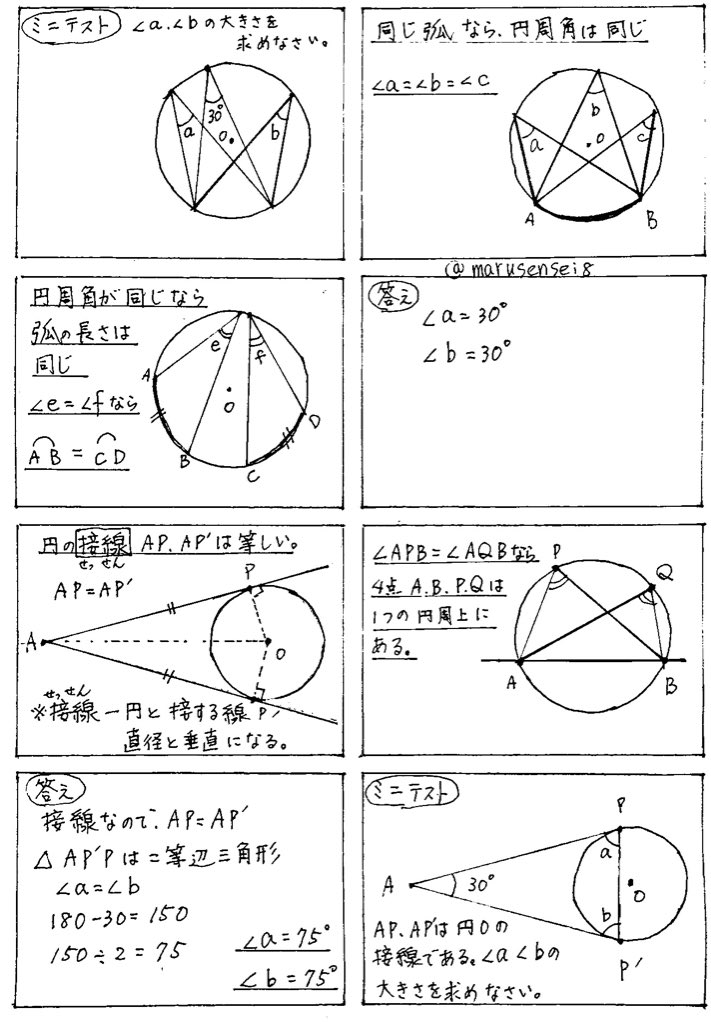
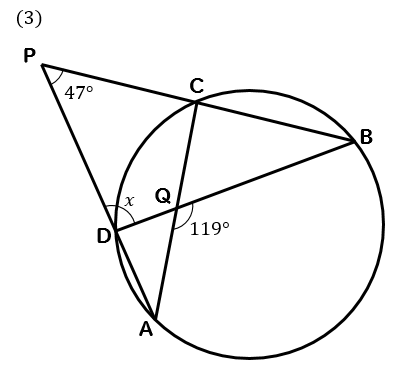
まず、円周角の定理 ① を使って \(∠cbd=∠cad=30°\) が求まります。 次に、点 \(a,e,d\) は一直線上にあるので、 \(∠bed=180°∠aeb=80°\) ここで「三角形の内角の合計は \(180°\)」という性質を使うと、\(∠adb=180°30°80°=70°\) と求まります。 あとは、\(∠adb\) は「弧 \(ab\) の円周角」・\(∠aob\) はなど 図形を総まとめ!小学校〜高校で習う各種公式重要記事一覧 練習問題②「円周上の \(\angle x\) を求める」 練習問題② 次の図で \(\angle x\) を求めよまずは、円周角の定理をおさらいしておきましょう! 同じ弧に対する中心角の大きさは円周角の大きさの2倍になる。 同じ弧に対する円周角の大きさは等しい この2つは円周角の定理の基本です。 必ず覚えておきましょうね! そして、次はブーメラン型
円周角の定理 指導案のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「円周角の定理 指導案」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「円周角の定理 指導案」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「円周角の定理 指導案」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「円周角の定理 指導案」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「円周角の定理 指導案」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「円周角の定理 指導案」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「円周角の定理 指導案」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「円周角の定理 指導案」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「円周角の定理 指導案」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円周角の定理 指導案」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「円周角の定理 指導案」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
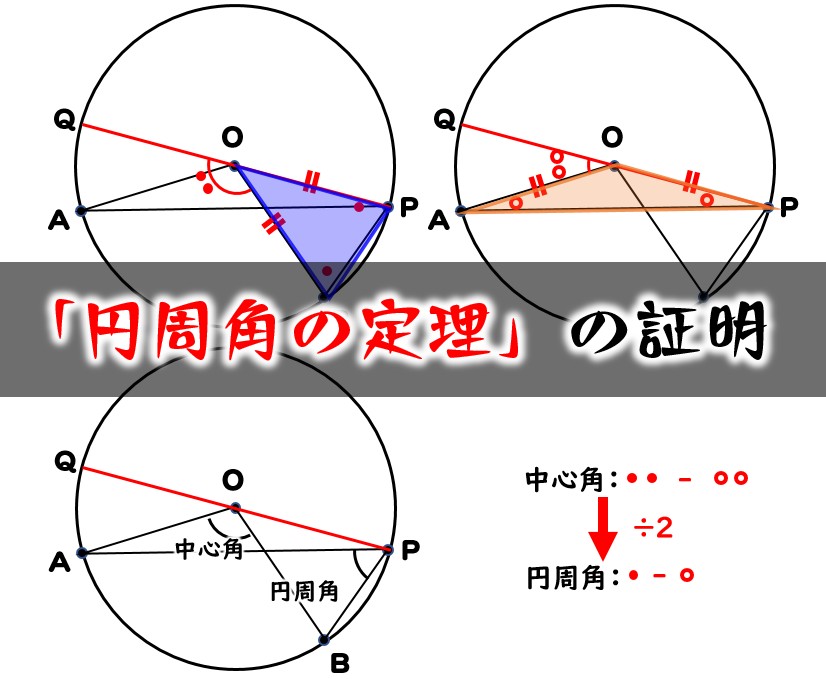
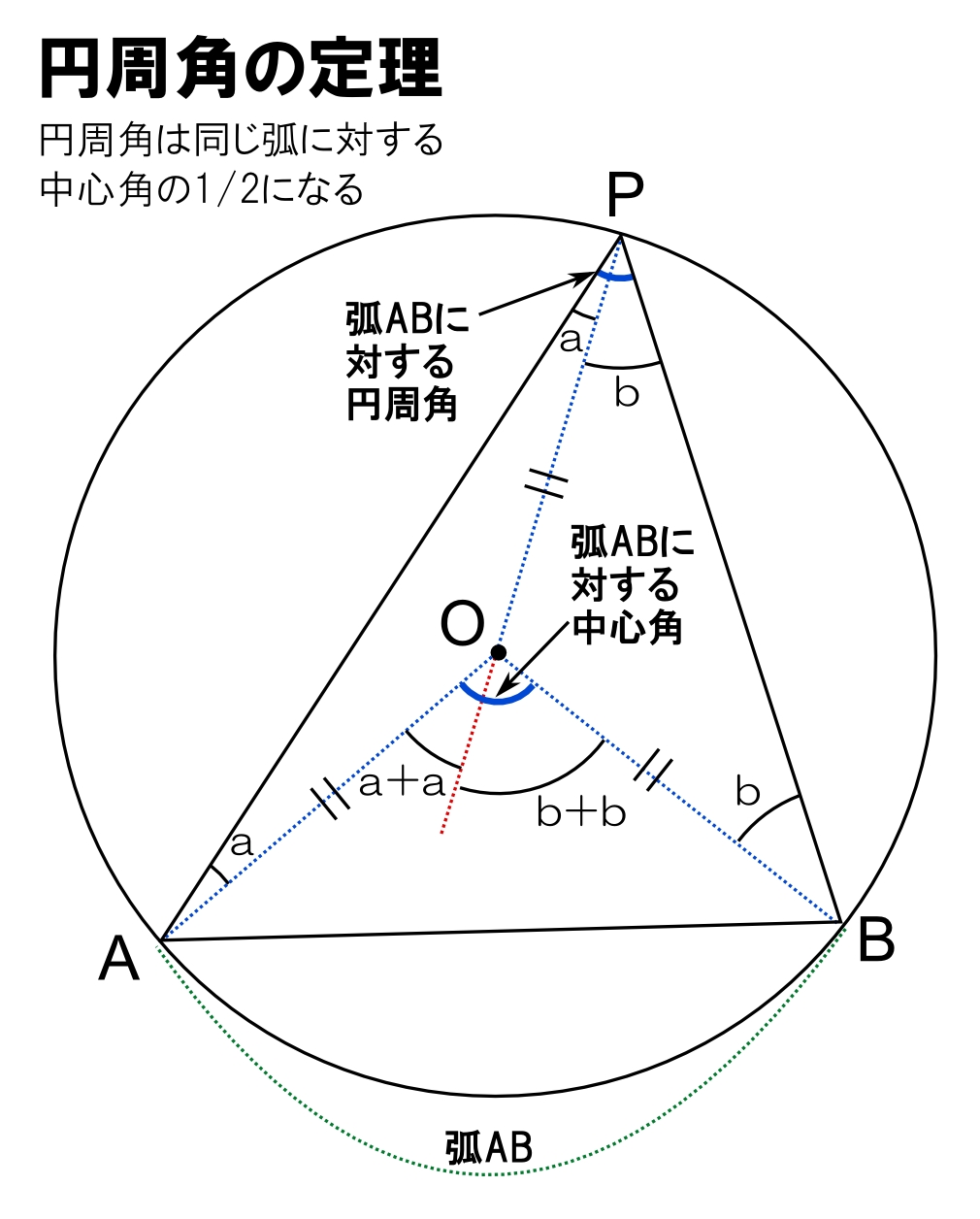
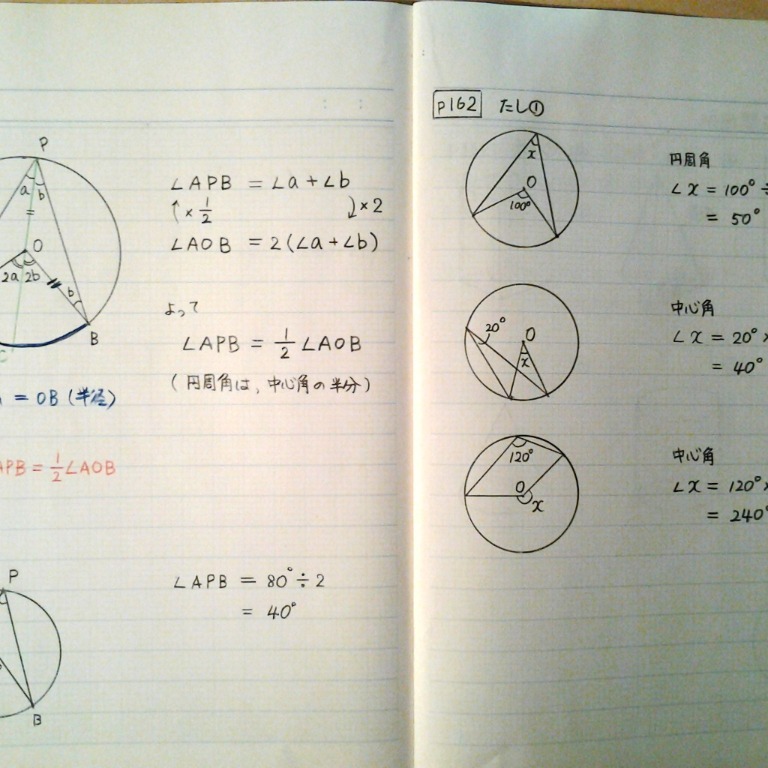
== 円周角の定理 == 円周角の定理 一つの弧に対する「円周角」の大きさは,「中心角」の半分になります. (証明) 1 右のようにACが中心を通るとき oc=ob= (半径)だから OBCは二等辺三角形になる. 二等辺三角形の2つの底角は等しいから ∠ b= ∠ c (1) 「三角形の外角は,それと隣り合わ3:円周角の定理を利用する。 この3つがポイントになります。 円の問題(方程式を使う) 円周上に点a、b、c、d、eがある。 線分dbは∠cdaの二等分線 線分ceは∠dcaの二等分線 ∠dac=30° のとき、∠eabの大きさを求めよ。 解説 答え:∠eab=105° 円の問題(気が付きにくい円周角と中心角) 点oを
Incoming Term: 円周角の定理, 円周角の定理 証明, 円周角の定理の逆, 円周角の定理の逆 証明, 円周角の定理 問題, 円周角の定理とは, 円周角の定理の逆 証明 転換法, 円周角の定理 練習問題, 円周角の定理 問題 難しい, 円周角の定理の逆 指導案, 円周角の定理 プリント, 円周角の定理 指導案,
コメント
コメントを投稿